Расстояние между горизонталями, так называемое заложение, показывает крутизну ската. Чем ближе друг к другу на карте расположены горизонтали, тем скат круче; чем больше расстояние между двумя соседними горизонталями, тем скат положе. Рассмотрим основные способы определения крутизны ската.
Вычислением. Измерив по карте заложение d и зная высоту сечения h, можно найти крутизну ската а по формуле
Эту формулу можно преобразовать, сделав некоторые допуски. Получится простая зависимость, справедливая для карт любого масштаба со стандартным сечением рельефа
a= 12/d,
где а — крутизна ската в градусах,
d — расстояние между двумя смежными горизонталями в миллиметрах.
С помощью линейки или на глаз. На топографических картах СССР стандартная высота сечения для каждого масштаба установлена такой, что заложению в 1 см соответствует крутизна около Г. В приведенной выше формуле существует обратная зависимость между заложением d и крутизной а. Поэтому можно вывести следующее правило: во сколько раз заложение меньше (или больше) одного сантиметра, во столько раз крутизна ската больше (или меньше) одного градуса. Отсюда следует, что заложению в 1 мм соответствует крутизна ската 10°, заложению в 2 мм — 5°, заложению в 5 мм—2° и т. д. Это правило позволяет определять крутизну скатов как по линейке с миллиметровыми делениями, так и на глаз.
По шкале заложений. На картах шкала заложений дается в виде графика, показанного на рис. 30. Вдоль горизонтального основания шкалы подписаны цифры, означающие крутизну скатов в градусах. На перпендикулярах к основанию отложены соответствующие им заложения и концы их соединены непрерывной кривой. Шкала заложений дается для двух высот сечений: одна — для заложений между двумя соседними горизонталями, другая для заложений между утолщенными.
Для определения крутизны ската по шкале заложений следует измерить циркулем расстояние между двумя смежными горизонталями и приложить циркуль к шкале заложений. Отсчет внизу на шкале против ножки циркуля укажет крутизну ската в градусах.
Теперь представьте себя в роли проектировщика автомобильной дороги. Перед вами карта, часть которой показана на рис. Требуется выбрать трассу дороги на участке от селения в левом нижнем углу карты до перевала между высотой с отметкой 249,2 и высотой с вышкой. Угол наклона дороги нигде не должен превышать 2°.
Возьмем по шкале заложений раствор .циркуля, соответствующий 2°. Этим раствором циркуля опишем дугу. из начальной точки А до пересечения со второй горизонталью в точке В и соединим эти две точки. Затем из точки В тем же радиусом опишем дугу до пересечения с третьей горизонталью и так далее, пока радиус не коснется горизонтали в конечной точке маршрута. Полученные точки пересечения радиусов с горизонталями соединим сплошной линией с плавными закруглениями. Эта кривая линия на всем протяжении будет иметь подъем ровно 2°.
Строители дорог очень часто сталкиваются с подобными задачами. Причем величину наклона земной поверхности они характеризуют так называемым уклоном.
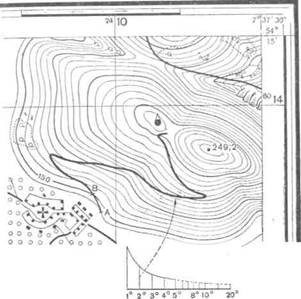
Рис. Шкала заложений.
Уклон обычно выражается десятичной дробью в тысячных долях. Например, уклон, равный 26, означает, что на каждые 1000 м расстояния местность повышается (или понижается) на 26 м.
У железнодорожного полотна часто можно видеть столбы с табличками. Наклон таблички указывает подъем или спуск, а цифры на ней выражают величину уклона и расстояние, на каком происходит этот уклон. Например тот означает, что на каждые 1000 м железнодорожное полотно повышается (или понижается) на 26 м и что такой уклон продолжается 1300 м. При этом 26 представляет сокращенную запись, заменяющую 0,026.
Чем же отличается уклон от крутизны ската и можно ли перевести величину уклона в градусные измерения, которыми выражается крутизна ската.
Между уклоном и крутизной существует очень простая математическая зависимость:
h/d= tg a
Поэтому, зная это отношение, можно легко определить угол а (крутизну ската) с помощью математических таблиц. Впрочем перевод вы можете сделать и без таблиц, если помните, что tg1 = 1/57, или 0,018. Следовательно, уклон в 26 тысячных, который дан в нашем примере, соответствует углу примерно в 1,5 градуса
(26/18=1.5)
назад вперед